
Для удобства
"Краткие сведения из теории стрельбы"
на сайте pro-tank.ru разбиты на три страницы
ЧТО ТАКОЕ ВЫСТРЕЛ И КАК ОН ПРОИСХОДИТ
Чтобы выстрелить, стрелок должен вложить патрон в ствол, закрыть затвор и произвести спуск ударника с бойком. Боек, ударяя по капсюлю-воспламенителю, вызывает его взрыв, от которого зажигается и сгорает воспламенитель. Воспламенитель, сгорая, поджигает боевой заряд. При сгорании боевого заряда образуется большое количество нагретых пороховых газов, обладающих большой упругостью. Пороховые газы давят с большой силой во все стороны, т. е. на стенки ствола, затвор и снаряд, рис. 49 (в дальнейшем изложении под термином "снаряд" подразумеваются как артиллерийские снаряды, так и пули.)
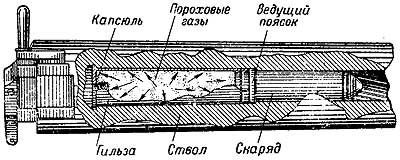
Рис.49. Действие пороховых газов во время выстрела
Так как стенки и затвор ствола делаются прочными, то пороховые газы устремляются по каналу ствола вперед, толкая перед собой снаряд. Под давлением пороховых газов снаряд врезается ведущим пояском в нарезы и, вращаясь в силу этого вокруг своей оси, двигается со все возрастающей скоростью по каналу ствола к дульному срезу. Снаряд покидает дульный срез канала ствола с большой скоростью, полученной им под действием пороховых газов; эта скорость называется начальной скоростью.
Вслед за снарядом вырываются пороховые газы, и раздается сильный звук. Совокупность всех описанных явлений и называется выстрелом. При выстреле пороховые газы давят и назад на затвор; так как в этом направлении пороховые газы не имеют выхода, то они толкают оружие назад. Этот толчок пороховых газов на затвор называется отдачей. У орудий отдача поглощается противооткатным устройством. У автоматического оружия энергия отдачи используется на выбрасывание гильзы, на заряжание оружия новым патроном и на производство следующего выстрела. У стрелкового оружия (винтовки,
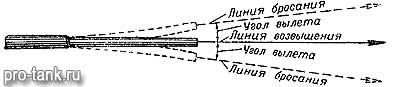
Рис.50. Колебания ствола во время выстрела
револьвера) энергия отдачи поглощается плечом или рукой стрелка. Снаряд вылетает из канала ствола по направлению продолженной оси канала ствола, называемой линией бросания (рис. 50). Линия бросания вследствие отдачи и колебаний ствола оружия в момент выстрела не совпадает с продолжением оси канала ствола наведенного оружия. Она отклоняется вниз или вверх на угол, который называется углом вылета. Угол вылета для различных образцов и даже экземпляров оружия различный.
ПОЛЕТ СНАРЯДА В ВОЗДУХЕ
Если бы на вылетевший из канала ствола снаряд не действовали различные силы, то снаряд продолжал бы свой полет по прямой линии, являющейся продолжением оси канала ствола, и

Рис.51. Траектория полета снаряда (пули) в воздухе
с той начальной скоростью, которую он получил под действием пороховых газов. Но снаряд имеет вес и, следовательно, на него за все время полета действует сила тяжести, которая притягивает его к земле. Поэтому-то снаряд летит не по прямой, а по кривой линии. Путь летящего снаряда называют траекторией (рис. 51).
Кроме того, на снаряд действует сила сопротивления воздуха. Под действием этой силы снаряд теряет свою скорость, а следовательно, и дальность полета. Кроме того, сила сопротивления воздуха стремится опрокинуть снаряд головной частью назад, т. е. заставить его "кувыркаться" (рис. 52), что ведет к неправильному полету снаряда, а следовательно, к потере скорости и уменьшению дальности полета.
Уничтожить силу сопротивления воздуха нельзя, но уменьшить ее действие на снаряд можно. Для этого снаряду придают наивыгоднейшую "обтекаемую" форму (головная часть заострена, запоясковая - скошена). Для того чтобы не допустить "кувыркания", снаряду придают быстрое вращательное движение вокруг собственной оси, что придает ему устойчивость в полете. Действие вращательного движения на устойчивость снаряда в полете
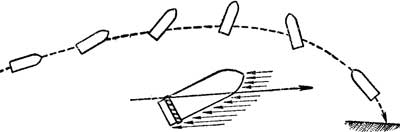
Рис.52. Действие силы сопротивления воздуха на снаряд (пулю)
можно легко понять, если вспомнить детскую игрушку - "волчок". Известно, что быстро вращающийся "волчок" может стоять на своей острой ножке. Как только вращение прекратится, он теряет устойчивость и падает набок. Вращательное движение снаряду придают нарезы в канале ствола и ведущий поясок на снаряде. Если посмотреть на траекторию снаряда сверху, то окажется, что она является не прямой линией по отношению к вертикальной плоскости, проходящей через продолженную ось канала ствола, а кривой. Отклонение траектории снаряда от плоскости стрельбы называется деривацией.
Деривация является следствием вращательного движения снаряда при полете его в воздухе. Деривация происходит в ту же сторону, в какую вращается снаряд. В нашем оружии нарезы идут слева вверх направо, поэтому снаряд отклоняется всегда вправо От плоскости стрельбы. Величина деривации увеличивается с увеличением дальности стрельбы. Поэтому при стрельбе, особенно на большие дальности, оружие направляют левее цели, учитывая величину деривации.
ЭЛЕМЕНТЫ ТРАЕКТОРИИ
Точкой вылета снаряда считают центр дульного среза канала ствола О (рис. 53) в момент вылета снаряда.
Горизонтом оружия называется горизонтальная плоскость OA, проходящая через точку вылета.
Линией возвышения называется продолженная ось канала ствола ОБ наведенного оружия.
Линией бросания называется продолженная ось канала ствола ОБ' в момент вылета снаряда.
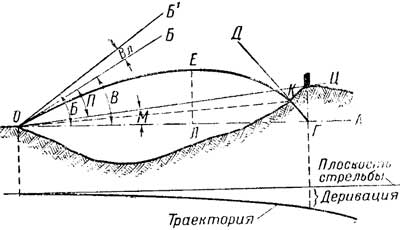
Рис.53. Элементы траектории
Линией цели называется прямая ОЦ, соединяющая точку вылета с целью.
Линией разрыва называется прямая OК, соединяющая точку вылета с точкой разрыва снаряда.
Углом возвышения В называется угол, образованный горизонтом оружия и линией возвышения.
Углом бросания Б называется угол, образованный горизонтом оружия и линией бросания.
Углом вылета Вл называется угол, образованный линией возвышения и линией бросания.
Углом места цели М называется угол, образованный горизонтом оружия и линией цели.
Углом прицеливания II называется угол, образованный линией цели и линией возвышения.
Вершиной траектории называется наивысшая точках Е подъема снаряда над горизонтом.
Высотой траектории называется вертикальное расстояние ЕЛ от вершины траектории до горизонта оружия.
Точкой падения называется точка К пересечения траектории с поверхностью земли.
Точкой встречи называется точка пересечения траектории с поверхностью цели.
Углом падения называется угол ДКО, образованный линией разрыва ОК и касательной к траектории ДК в точке падения.
Углом встречи называется угол ЗРА, образованный поверхностью цели (или земли) с касательной к траектории в точке падения (рис. 54).
Окончательной скоростью называется скорость снаряда в точке падения его.
Дальностью называется расстояние ОЦ между целью и оружием по линии цели.
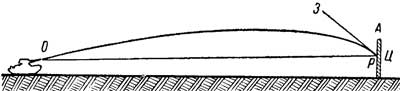
Рис.54. Точка встречи и угол встречи
Горизонтальной дальностью называется расстояние ОГ от оружия до цели, считая по горизонту.
ПОРАЖАЕМОЕ ПРОСТРАНСТВО. ПРЯМОЙ ВЫСТРЕЛ.
МЕРТВОЕ ПРОСТРАНСТВО
Форма траектории зависит от начальной скорости снаряда и от углов бросания.
Чем меньше начальная скорость снаряда, тем больший угол бросания нужно придавать оружию и тем больше будет подниматься траектория над линией цели. Поэтому различное оружие при стрельбе на одну и ту же дальность может давать различные траектории: одно оружие - крутую траекторию, другое оружие - пологую (рис. 55).

Рис.55. Формы траекторий
При стрельбе из одного и того же оружия на различные дальности форма траектории также изменяется: чем больше дальность стрельбы, тем круче траектория, и наоборот (рис. 56). Прицельным поражаемым пространством называется расстояние, на протяжении которого траектория не поднимается над линией цели выше данной цели (рис. 56).
Чем выше цель, тем больше прицельное поражаемое пространство.
Цель, находящаяся в любой точке прицельного поражаемого пространства, будет поражаться без изменения установки прицела и точки наводки. Поэтому при стрельбе по вертикальным целям выгодно иметь оружие с пологой траекторией.
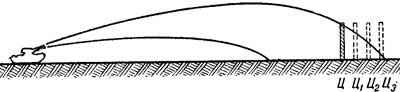
Рис.56. Прицельное поражаемое пространство (расстояние Ц-Ц3)
Если прицельное поражаемое пространство для цели данной высоты равняется дальности до цели (рис. 57), то эта дальность называется дальностью прямого выстрела. Выстрел, произведенный по цели, находящейся в пределах дальности прямого выстрела, называется прямым выстрелом.

Рис.57. Дальность прямого выстрела
Очевидно, что дальность прямого выстрела тем больше, чем более полога траектория и выше цель. При стрельбе по целям, находящимся в пределах дальности прямого выстрела, менять установку прицела или точку наводки не нужно, так как цель будет поражаться при установке прицела, равного дальности прямого выстрела.
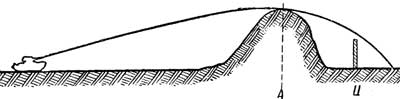
Рис. 58. Мертвое пространство (расстояние А-Ц)
Дальности прямого выстрела из танкового пулемета (в метрах) по целям
|
Головным
|
Грудным
|
Поясным
|
В рост
|
По коннице
|
|
300
|
400
|
550
|
700
|
750
|
Дальности прямого выстрела из танковых пушек (в метрах)
|
Оружие и снаряд
|
По целям высотой
|
||
|
1 метр
(ПТОР) |
1,5 метра
(орудие ПА) |
2 метра
(малый танк) |
|
| 37-миллиметровая пушка Гочкиса |
400
|
450
|
500
|
|
45-миллиметровая пушка
|
|||
| Осколочная граната |
200
|
300
|
350
|
| Бронебойная |
600
|
700
|
800
|
| 76-миллиметровая пушка |
350
|
400
|
150
|
Участок местности, на протяжении которого цель, прикрытая преградой, не поражается, называется мертвым пространством (рис. 58). Величина мертвого пространства зависит от формы траектории и высоты преграды. Чем круче траектория и ниже преграда, тем меньше мертвое пространство, и наоборот. Для стрельбы по целям, находящимся за преградами, выгодно пользоваться оружием с крутой траекторией.
ИЗМЕРЕНИЕ УГЛОВ
В военном деле для быстроты расчетов углы измеряются не в градусах, минутах и секундах, а в делениях угломера. Одно малое деление угломера называют тысячной. Из геометрии известно, что окружность заключает в себе 360°. Это значит, что дуга, соответствующая углу в 1°, составляет 1/360 часть окружности. Мера же угла - тысячная получается из того расчета, что окружность делится на 6000 частей. Если 360° (что составляет 21600 минут) разделить на 6 000, то
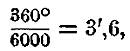
 |
т. е. одна тысячная соответствует (равна) 3',6.
Тысячная обладает еще одним замечательным свойством.
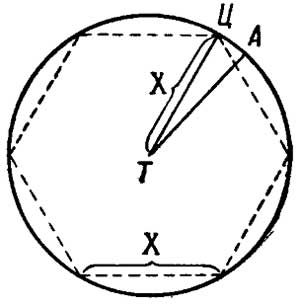
Опишем из точки нахождения оружия Т (рис. 59) окружность радиусом X, равным дальности до цели. Из точки нахождения цели Ц будем откладывать по окружности радиусы X. Как известно, на окружности уложится 6Х, т. е. 6 дальностей до цели. Примем за длину окружности не самую окружность, а вписанный в нее шестиугольник, т. е. 6Х, и разделим всю окружность на 6000 равных дуг. Тогда каждая такая дуга (положим ЦА) будет равна одной тысячной части радиуса, т. е.
![]()
Прицелы для измерения углов в горизонтальной плоскости имеют в поле зрения шкалу боковых поправок, называемую целиком (рис. 60). Расстояние между двумя черточками этой шкалы равно 4 тысячным. Следовательно, если снаряд при стрельбе на 800 метров разорвался правее прицельного перекрестия прицела на три деления шкалы целика, то это означает, что разрыв произошел правее цели на 12 тысячных, или же, в метрах, на
![]()
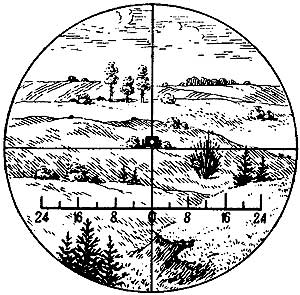
Рис. 60. Наблюдение разрывов через прицел
РАССЕИВАНИЕ ВЫСТРЕЛОВ И ПРИЧИНЫ, ВЫЗЫВАЮЩИЕ РАССЕИВАНИЕ
Произведем серию выстрелов по вертикальному щиту из пушки танка, стоящего на месте. Каждый из выстрелов будем производить при возможно одинаковых условиях и при самой тщательной наводке в центр щита. И все же, несмотря на соблюдение одинаковых условий для каждого выстрела, щит окажется пробитым

Рис.61. Рассеивание выстрелов при стрельбе с места (0АА1- средняя траектория
А и А1- средние точки попадания
не в одном, а в разных местах - выше и ниже, вправо и влево от центра щита. Пробив щит, снаряды упадут на землю, и опять-таки в разных местах - один ближе к щиту, другие - дальше, третьи - правее и четвертые - левее (рис. 61). Это происходит потому, что снаряды в силу ряда причин летят не по одной траектории, а каждый снаряд имеет свою собственную траекторию.
Таким образом, при производстве по одной и той же цели и при одних и тех же условиях некоторого количества выстрелов всегда будет получаться не одна траектория, а пучок или сноп траекторий, расходящийся от дульного среза ствола. Подобное явление носит название рассеивания выстрелов.
Воображаемая траектория OAA1, проходящая в центре пучка траекторий, называется средней траекторией. Все таблицы стрельб дают расчеты применительно к средней траектории.
Точка пересечения средней траектории с вертикальным щитом А или с горизонтальной поверхностью земли А1 называется средней точкой попадания.
Рассеивание выстрелов при стрельбе с места зависит от следующих причин:
1. Снаряды при вылете из канала ствола орудия имеют различные начальные скорости.
Различные начальные скорости снаряды получают по следующим причинам:
а) снаряды, несмотря на тщательное изготовление, все же отличаются друг от друга по весу и по форме;
б) при выстреле в силу допусков в размерах ведущего пояска и гильзы снаряд неодинаково досылается в камору;
в) боевые заряды, несмотря на тщательное их изготовление и взвешивание, отличаются друг от друга как по весу, так и по своему действию.
2. При стрельбе получаются разные углы бросания, что имеет место в результате:
а) разнообразия углов вылета;
б) разнообразия наводки;
в) наличия мертвых ходов в подъемном механизме, поворотном механизме и механизмах прицела.
3. Различия условий полета снарядов в воздухе.
Атмосферные условия никогда не остаются одинаковыми для различных выстрелов. Особенно быстро и резко изменяется ветер. Кроме того, снаряды имеют неодинаковый вес и форму, что влияет на сопротивление, оказываемое воздухом снаряду при его полете. При стрельбе с хода рассеивание выстрелов увеличивается.
Происходит это потому, что корпус боевой машины во время движения испытывает качку. Следовательно, за время запаздывания выстрела (Временем запаздывания выстрела считается время от момента оконча-ввя наводки до момента вылета снаряда из канала ствола) в силу прекращения наводки ствол оружия вместе с корпусом танка отклоняется от заданного направления и тем увеличивает рассеивание выстрелов.
Так как корпус боевой машины испытывает качку по всем направлениям, то очевидно, что при стрельбе с хода рассеивание выстрелов будет увеличиваться тоже по всем направлениям.
По сравнению со стрельбой с места линейная величина рассеивания при стрельбе с хода увеличивается от 2 до 3 раз, а площадь рассеивания соответственно увеличивается от 4 до 9 раз.
Устранить рассеивание выстрелов невозможно, поскольку нельзя устранить причины, вызывающие рассеивание. Можно только уменьшить рассеивание, уменьшив действие причин, вызывающих его.
Уменьшение рассеивания выстрелов при стрельбе с места достигается:
а) подбором для стрельбы боевых зарядов одной партии и одинакового веса;
б) тщательной и однообразной наводкой при каждом выстреле;
в) устранением мертвых ходов механизмов наводки и однообразным подведением маховиков механизмов всегда с одной и той же стороны (снизу вверх);
г) правильным уходом за каналом ствола и механизмами оружия.
Если стрельба ведется с хода, уменьшению рассеивания выстрелов способствуют:
а) уменьшением качки корпуса боевой машины, что достигается правильным вождением боевой машины и замедлением ее хода при производстве выстрела;
б) уменьшением времени запаздывания выстрела, что достигается правильной отладкой спусковых механизмов;
в) производством выстрела с упреждением, т. е. нажатием на педаль ножного спуска или спусковой крючок не в тот момент, когда изображение цели совместилось с прицельным перекрестием, а несколько раньше, для того чтобы снаряд покинул канал ствола точно в момент совмещения изображения цели с прицельным перекрестием.
Стрелок должен стремиться к уменьшению рассеивания выстрелов и к совмещению средней точки попадания с центром цели, что возможно при отличном знании своего оружия, правил и приемов стрельбы.
ЗАКОН РАССЕИВАНИЯ И ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ РАССЕИВАНИЕ
Пробоины на щите, полученные в результате серии выстрелов, располагаются в определенном порядке, подчиняясь действию закона, называемого законом рассеивания.
Основные положения закона рассеивания таковы:
а) пробоины на щите располагаются на определенной площади, за пределами которой пробоин не будет;
б) вокруг средней точки попадания пробоины располагаются гуще, чем по краям (рис. 62);
в) если через среднюю точку попадания провести вертикальную линию, то по обеим сторонам от нее количество пробоин будет одинаковое; одинаковое же количество пробоин будет по обе стороны от горизонтальной линии, проведенной через среднюю точку попадания (рис. 62, а).
Для измерения рассеивания пользуются сердцевинной полосой и сердцевиной.
Сердцевинной полосой называют полосу, которая вмещает 70% всех пробоин и своей серединой совмещается с линией, проходящей через среднюю точку попадания (рис. 62, а, б).
Вертикальная площадь рассеивания содержит по высоте и ширине по три сердцевинных полосы.
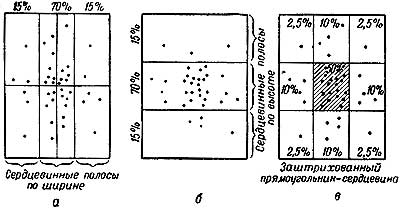
Рис.62. Закон рассеивания выстрелов
Прямоугольник, образованный пересечением вертикальной и горизонтальной сердцевинных полос в центре площади рассеивания, называется сердцевиной (рис. 62, в). Сердцевина вмещает 50% всех попавших снарядов. Другая половина снарядов распределяется по остальным восьми прямоугольникам, образованным пересечением сердцевинных полос, причем в крайних угловых прямоугольниках будет вмещаться по 2,5% всех попавших снарядов, а в крайних средних прямоугольниках - по 10% всех попавших снарядов (рис. 62, в).
Места падения снарядов на горизонтальный участок местности будут тоже подчиняться закону рассеивания, причем ширина площади рассеивания будет равна ширине площади рассеивания на вертикальном щите, длина же будет значительно больше.
Рассеивание на горизонтальном участке местности точно так же измеряется сердцевинными полосами по ширине и по дальности и сердцевиной.
Сердцевинные полосы и сердцевины для одного и того же оружия и снаряда на разных дальностях неравны, потому что траектории идут расходящимся пучком.
Величина сердцевинных полос по ширине, высоте и дальности обычно дается в таблицах стрельбы.
РАСЧЕТ ВОЗМОЖНОГО ЧИСЛА ПОПАДАНИЙ
Зная закон рассеивания, величину рассеивания и положение средней точки попадания по отношению к цели, стрелок может заранее рассчитать число попаданий, которое можно в среднем ожидать при стрельбе по заданной цели.
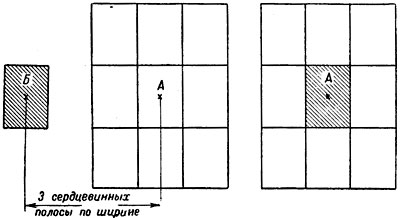
Рис. 63. Подсчет возможного числа попаданий
(заштрихованный прямоугольник - цель,
незаштрихованный - площадь рассеивания;
А - средняя точка попадания; Б - центр цели).
 |
Действительно, если средняя точка попадания находится на уровне центра цели, но правее ее на три сердцевинных полосы, то можно заранее сказать, что ни один снаряд в цель не попадет (рис. 63, а). Если же средняя точка попадания совпадает с центром цели и цель по величине равна сердцевине (рис. 63, б), то очевидно, что из всего числа выпущенных снарядов в цель попадет 50%, т. е. половина.
Для подсчета количества попаданий, которое в среднем можно ожидать при стрельбе по данной цели на заданной дальности стрельбы, поступают так.
Вычерчивают в произвольном масштабе площадь рассеивания (рис. 64). Далее, в том же масштабе, на площадь рассеивания наносят площадь цели, причем со средней точкой попадания совмещается точка цели, через которую проходит средняя траектория.
Затем, считая, что в каждом прямоугольнике площади рассеивания, образованном пересечением сердцевинных полос, пробоины располагаются равномерно, подсчитывают по отношению площади цели к площади рассеивания возможное число попаданий.
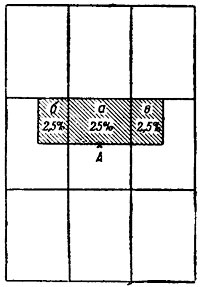
Пример. Пусть площадь рассеивания по отношению к площади цели располагается так, как показано на рис. 80. Очевидно, что в часть площади а попадает 25% выпущенных снарядов, так как она наполовину меньше сердцевины; в части же площади б в в попадает по 2,5% выпущенных снарядов, так как эти части площади цели в четыре раза меньше соответствующих прямоугольников площади рассеивания, образованных пересечением сердцевинных полос. Таким образом, общий ожидаемый процент попадания будет равен:
25% + 2,5% + 2,5% = 30%
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ТОЧКИ ПОПАДАНИЯ
Для того чтобы найти установки прицела и целика, при которых средняя точка попадания будет совмещаться с центром мишени, стрелку нужно будет определять среднюю точку попадания.
При наличии двух пробоин средняя точка попадания определяется так. Обе пробоины соединяются прямой линией, которую затем делят пополам (рис. 65, а). Середина этой линии (точка А) и будет средней точкой попадания для двух пробоин.
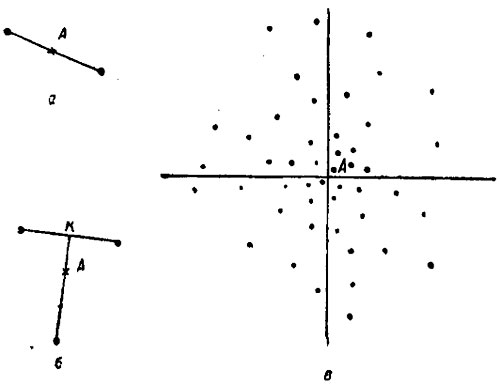
Рис.65. Определение средней точки попадания
Среднюю точку попадания трех пробоин определяют таким образом (рис. 65, б). Соединяют две близлежащие пробоины прямой линией, которую затем делят пополам. От точки деления (точки К) проводят линию к третьей пробоине и делят эту линию на три равные части. Точка деления, находящаяся ближе к первой линии, и будет средней точкой попадания (точка А) для трех пробоин.
При большом количестве пробоин среднюю точку попадания находят следующим образом (рис. 65, в). Проводят на щите вертикальную линию так, чтобы справа и слева от нее было одинаковое количество пробоин. Затем проводят горизонтальную линию, причем выше и ниже ее тоже должно быть одинаковое количество пробоин. Точка пересечения вертикальной и горизонтальной линий и будет средней точкой попадания.
